HOLAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

HOLAAAAAA! Somos Mica & Vero, y bueno como sabemos mucho sobre Matematica :/ , les vamos a enseñar un poco. Pueden pedir de que tema quieren que hagamos la proxima entrada. Aca estan las opciones:
-Geometria
-Funciones
-Ecuaciones

Bueno y hoy para empezar bien arriba con el blog les dejamos la teoria sobre proporcionalidad :D
Cualquier consulta, mandenos un mensaje o dejenos un comentario con sus dudas.

PROPORCIONALIDAD

La proporcionalidad es una relación entre magnitudes medibles. Es uno de los escasos conceptos matemáticos ampliamente difundido en la población. Esto se debe a que es en buena medida intuitiva y de uso muy común. La proporcionalidad directa es un caso particular de las variaciones lineales. El factor constante de proporcionalidad puede utilizarse para expresar las relaciones entre las magnitudes.

Ejemplo 1:

La receta de un pastel de vainilla indica que para cuatro personas se necesitan 200 g de harina, 150 g de mantequilla, cuatro huevos y 120 g de azúcar. ¿Cómo adaptar la receta para cinco personas? Según varios estudios, la mayoría de la gente calcularía las cantidades para una persona (dividiendo entre cuatro) y luego las multiplicaría por el número real de personas, cinco, otras solo le sumarían lo que a una persona le corresponde. Una minoría no siente la necesidad de pasar por las cantidades unitarias (es decir por persona) y multiplicaría los números de la receta por 5/4 = 1,25 (lo que equivale a añadir cinco huevos, 250 g de harina; 187,5 g de mantequilla y 150 g de azúcar tendrá el mismo sabor que el otro, si el cocinero aficionado se muestra tan bueno como el chef que escribió la receta.

Se dice que la cantidad de cada ingrediente es proporcional al número de personas y se representa esta situación mediante una tabla de proporcionalidad: coeficiente k no nulo ( en el ejemplo) tal que

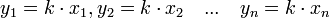
Si se consideran e 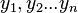como valores de variables e 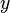, entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.
La representación gráfica de esta funcion es una receta que pasa por el origen del sistema de coordenadas. Una variación (incremento o decremento) de x da lugar a una variación proporcional de y (y recíprocamente, puesto que k≠0: y = 1/k · x):

Son las funciones más sencillas que existen y las primeras que se estudian en clase de matemáticas, con alumnos de trece años aproximadamente.

La relación «Ser proporcional a» es

• reflexiva ( toda variable es proporcional a sí misma, con el coeficiente 1)
• simétrica (cuando y es proporcional a x entonces x lo es a y, con el coeficiente inverso) y
• transitiva (si x es proporcional a y, e y a z, entonces x lo es con z, multiplicando los coeficientes)

por lo que se trata de una relación de equivalencia. En particular dos variables proporcionales a una tercera serán proporcionales entre sí).

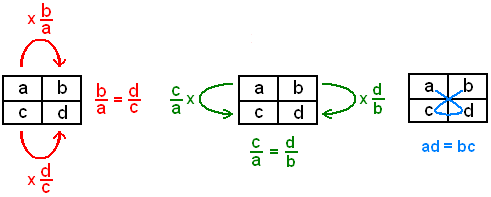
La tabla del primer ejemplo se puede descomponer en tres de formato dos por dos:

por tanto las propiedades de la proporcionalidad se ilustran preferentemente con tablas de cuatro casillas.

Una proporción está formada por los números a, b, c y d, si la razón entre a y b es la misma que entre c y d.

Una proporción está formada por dos razones iguales:

a : b = c : d

Dónde a, b, c y d son distintos de cero y se lee a es a b como c es a d .

Proporción múltiple:

Una serie de razones está formada por tres o más razones iguales:

a : b = c : d = e : f

Y se puede expresar como una proporción múltiple:

a : c : e = b : d : f

En la proporción hay cuatro términos; a y d se llaman extremos; c y b se llaman medios.

En toda proporción el producto de los extremos es igual al producto de los medios.

Para establecer que una tabla es proporcional, se puede:

1. verificar que la segunda columna es múltiple de la primera, (primera tabla: para pasar de la primera casilla a la segunda, hay que multiplicar por ; en la segunda línea se tiene que multiplicar por , luego estas fracciones deben ser iguales para obtener columnas proporcionales)
2. verificar que la segunda línea es múltiple de la primera (segunda tabla, con un raciocinio parecido) o
3. verificar la igualdad de los productos cruzados: a·d = b·c. (tercera tabla: las igualdades anteriores equivalen a a·d = b·c, cuando no hay valores nulos, que por cierto no tienen un enorme interés en este contexto).